Clase 3
- Búsqueda
- Big O
- Búsqueda lineal
- Estructuras
- Ordenación
- Ordenación por selección
- Recursión
- Ordenación por mezcla
Búsqueda
- La última vez, hablamos sobre la memoria en un ordenador, o RAM, y sobre cómo nuestros datos se pueden almacenar como variables individuales o como matrices de muchos elementos o elementos.
- Podemos pensar en una matriz con una serie de elementos como una fila de casilleros, donde un ordenador solo puede abrir un casillero para mirar un elemento, uno a la vez.
- Por ejemplo, si queremos comprobar si un número está en una matriz, con un algoritmo que toma una matriz como entrada y produce un booleano como resultado, podríamos:
- mirar en cada casillero, o en cada elemento, uno a la vez, de principio a fin.
- Esto se llama búsqueda lineal, donde nos movemos en una línea, ya que nuestra matriz no está ordenada.
- empezar en el medio y movernos a la izquierda o a la derecha dependiendo de lo que estemos buscando, si nuestra matriz de elementos está ordenada.
- Esto se llama búsqueda binaria, ya que podemos dividir nuestro problema en dos con cada paso, como hizo David con la guía telefónica en la semana 0.
- mirar en cada casillero, o en cada elemento, uno a la vez, de principio a fin.
-
Podríamos escribir pseudocódigo para la búsqueda lineal:
Para i de 0 a n-1 Si el elemento i-ésimo es 50 Devolver verdadero Devolver falso- Podemos etiquetar cada uno de los
ncasilleros de0an-1y comprobar cada uno de ellos en orden.
- Podemos etiquetar cada uno de los
-
Para la búsqueda binaria, nuestro algoritmo podría ser:
Si no hay elementos Devolver falso Si el elemento central es 50 Devolver verdadero De lo contrario, si 50 < elemento central Buscar en la mitad izquierda De lo contrario, si 50 > elemento central Buscar en la mitad derecha- Finalmente, no nos quedará ninguna parte de la matriz (si el elemento que queríamos no estaba en ella), por lo que podemos devolver
falso. - De lo contrario, podemos buscar cada mitad dependiendo del valor del elemento central.
- Finalmente, no nos quedará ninguna parte de la matriz (si el elemento que queríamos no estaba en ella), por lo que podemos devolver
Notación Big O
- En la semana 0, vimos diferentes tipos de algoritmos y sus tiempos de ejecución:
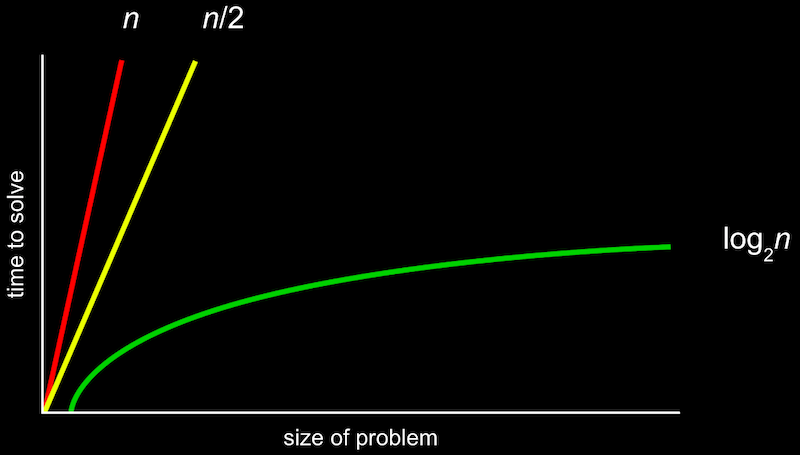
- La forma más formal de describir esto es con la notación O grande, que podemos considerar como "del orden de". Por ejemplo, si nuestro algoritmo es de búsqueda lineal, tomará aproximadamente O(n) pasos, "del orden de n". De hecho, incluso un algoritmo que observa dos elementos a la vez y toma n/2 pasos tiene O(n). Esto se debe a que, a medida que n aumenta, solo importa el término más grande, n.
- De manera similar, un tiempo de ejecución logarítmico es O(log n), sin importar cuál sea la base, ya que esto es solo una aproximación de lo que sucede con n muy grande.
- Hay algunos tiempos de ejecución comunes:
- O(_n_2)
- O(n log n)
- O(n)
- (búsqueda lineal)
- O(log n)
- (búsqueda binaria)
- O(1)
- Los informáticos también pueden utilizar la notación Ω grande, Omega grande, que es el límite inferior del número de pasos para nuestro algoritmo. (O grande es el límite superior del número de pasos, o el peor de los casos, que normalmente es lo que más nos importa). Con la búsqueda lineal, por ejemplo, el peor de los casos es n pasos, pero el mejor de los casos es 1 paso, ya que nuestro elemento podría ser el primer elemento que revisamos. El mejor de los casos para la búsqueda binaria también es 1, ya que nuestro elemento podría estar en el medio del arreglo.
- Y tenemos un conjunto similar de los tiempos de ejecución Ω grandes más comunes:
- Ω(_n_2)
- Ω(n log n)
- Ω(n)
- (contar el número de elementos)
- Ω(log n)
- Ω(1)
- (búsqueda lineal, búsqueda binaria)
Búsqueda lineal
-
Echemos un vistazo a
numbers.c:#include <cs50.h> #include <stdio.h> int main(void) { // Un arreglo de números int numbers[] = {4, 8, 15, 16, 23, 42}; // Busca el 50 for (int i = 0; i < 6; i++) { if (numbers[i] == 50) { printf("Encontrado\n"); return 0; } } printf("No encontrado\n"); return 1; } -
Aquí inicializamos un arreglo con algunos valores y verificamos los elementos del arreglo de uno en uno, en orden.
-
Y en cada caso, dependiendo de si el valor se encontró o no, podemos regresar un código de salida de 0 (para éxito) o 1 (para falla).
-
Podemos hacer lo mismo con nombres:
#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { // Un arreglo de nombres string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"}; // Busca EMMA for (int i = 0; i < 4; i++) { if (strcmp(names[i], "EMMA") == 0) { printf("Encontrado\n"); return 0; } } printf("No encontrado\n"); return 1; } -
No podemos comparar cadenas directamente, ya que no son un tipo de datos simple sino un arreglo de muchos caracteres, y necesitamos compararlos de manera diferente. Afortunadamente, la biblioteca
stringtiene una funciónstrcmpque compara cadenas por nosotros y regresa0si son iguales, por lo que podemos usarla. -
Intentemos implementar una agenda telefónica con las mismas ideas:
#include <cs50.h> #include <stdio.h> #include <string.h> int main(void) { string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"}; string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"}; for (int i = 0; i < 4; i++) { if (strcmp(names[i], "EMMA") == 0) { printf("Encontrado %s\n", numbers[i]); return 0; } } printf("No encontrado\n"); return 1; } -
Usaremos cadenas para los números de teléfono, ya que pueden incluir formato o ser demasiado largos para un número.
- Ahora, si el nombre en un determinado índice en el arreglo
namescoincide con el que estamos buscando, regresaremos el número de teléfono en el arreglonumbers, en el mismo índice. Pero eso significa que debemos tener especial cuidado para asegurarnos de que cada número corresponda al nombre en cada índice, especialmente si agregamos o eliminamos nombres y números.
Estructuras
-
Resulta que podemos crear nuestros propios tipos de datos personalizados llamados estructuras:
#include <cs50.h> #include <stdio.h> #include <string.h> typedef struct { string name; string number; } persona; int main(void) { persona people[4]; people[0].name = "EMMA"; people[0].number = "617–555–0100"; people[1].name = "RODRIGO"; people[1].number = "617–555–0101"; people[2].name = "BRIAN"; people[2].number = "617–555–0102"; people[3].name = "DAVID"; people[3].number = "617–555–0103"; // Buscar EMMA for (int i = 0; i < 4; i++) { if (strcmp(people[i].name, "EMMA") == 0) { printf("Encontrado %s\n", people[i].number); return 0; } } printf("No encontrado\n"); return 1; }- Podemos pensar en las estructuras como contenedores, dentro de los cuales hay múltiples otros tipos de datos.
- Aquí, creamos nuestro propio tipo con una estructura llamada
persona, que tendrá unstringllamadonamey unstringllamadonumber. Luego, podemos crear un arreglo de estos tipos de estructuras e inicializar los valores dentro de cada uno de ellos, utilizando una nueva sintaxis,., para acceder a las propiedades de cadapersona. - En nuestro ciclo, ahora podemos estar más seguros de que el
numbercorresponde alnameya que son del mismo elementopersona.
Ordenamiento
- Si nuestra entrada es una lista desordenada de números, hay muchos algoritmos que podríamos usar para producir una salida de una lista ordenada.
- Con ocho voluntarios en el escenario con los siguientes números, podríamos considerar intercambiar pares de números uno al lado del otro como primer paso.
-
Nuestros voluntarios comienzan en el siguiente orden aleatorio:
6 3 8 5 2 7 4 1 -
Observamos los dos primeros números y los intercambiamos para que estén en orden:
6 3 8 5 2 7 4 1 – – 3 6 8 5 2 7 4 1 -
El siguiente par,
6y8, están en orden, por lo que no necesitamos intercambiarlos. -
El siguiente par,
8y5, deben intercambiarse:3 6 8 5 2 7 4 1 – – 3 6 5 8 2 7 4 1 -
Continuamos hasta llegar al final de la lista:
3 6 5 2 8 7 4 1 – – 3 6 5 2 7 8 4 1 – – 3 6 5 2 7 4 8 1 – – 3 6 5 2 7 4 1 8 -
Nuestra lista aún no está ordenada, pero estamos un poco más cerca de la solución porque el valor más grande,
8, se ha desplazado hasta el final a la derecha. -
Repetimos esto con otra pasada por la lista:
3 6 5 2 7 4 1 8 – – 3 6 5 2 7 4 1 8 – – 3 5 6 2 7 4 1 8 – – 3 5 2 6 7 4 1 8 – – 3 5 2 6 7 4 1 8 – – 3 5 2 6 4 7 1 8 – – 3 5 2 6 4 1 7 8- Tenga en cuenta que no necesitamos intercambiar el 3 y el 6, o el 6 y el 7.
-
Ahora, el siguiente valor más grande,
7, se movió hasta el final a la derecha. Si repetimos esto, cada vez más partes de la lista se ordenan y rápidamente tenemos una lista completamente ordenada. -
Este algoritmo se llama ordenamiento de burbuja, donde los valores grandes "burbujean" hacia la derecha. El pseudocódigo para esto podría verse así:
Repetir n–1 veces Para i de 0 a n–2 Si los elementos i y i+1 están fuera de orden Intercambiarlos- Como estamos comparando el elemento
iyi+1, solo necesitamos subir hasta n – 2 parai. Luego, intercambiamos los dos elementos si están fuera de orden. - Y podemos detenernos después de haber realizado n – 1 pasadas, ya que sabemos que los n–1 elementos más grandes habrán burbujeado hacia la derecha.
- Como estamos comparando el elemento
-
Tenemos n – 2 pasos para el bucle interno y n – 1 bucles, por lo que obtenemos un total de n_2 – 3_n + 2 pasos. Pero el factor más grande, o término dominante, es n_2, a medida que
naumenta más y más, por lo que podemos decir que el ordenamiento de burbuja es _O(_n_2). - Hemos visto tiempos de ejecución como los siguientes, por lo que aunque la búsqueda binaria es mucho más rápida que la búsqueda lineal, es posible que no valga la pena el costo único de ordenar la lista primero, a menos que hagamos muchas búsquedas con el tiempo:
- O(_n_2)
- Ordenamiento de burbuja
- O(n log n)
- O(n)
- Búsqueda lineal
- O(log n)
- Búsqueda binaria
- O(1)
- O(_n_2)
- Y Ω para el ordenamiento de burbuja sigue siendo n_2, ya que todavía comprobamos cada par de elementos para _n – 1 pasadas.
Selección de tipo
-
Podemos elegir otro enfoque con el mismo conjunto de números:
6 3 8 5 2 7 4 1 -
En primer lugar, consideraremos cada uno de los números y recordaremos el más pequeño que hayamos visto. Entonces, podemos canjearlo con el primer número en nuestra lista, ya que sabemos que es el más pequeño:
6 3 8 5 2 7 4 1 – – 1 3 8 5 2 7 4 6 -
Ahora sabemos que al menos el primer elemento de nuestra lista está en el lugar correcto, por lo que podemos seleccionar el elemento más pequeño entre el resto y canjearlo con el siguiente elemento no ordenado (ahora el segundo elemento):
1 3 8 5 2 7 4 6 – – 1 2 8 5 3 7 4 6 -
Podemos repetir esto una y otra vez hasta que tengamos una lista ordenada.
-
Este algoritmo se llama selección de tipo, y podríamos escribir el pseudocódigo de la siguiente manera:
Para i de 0 a n–1 Encontrar el elemento más pequeño entre el elemento i y el último elemento Canjear el elemento más pequeño con el elemento i -
Con la notación O grande, todavía tenemos un tiempo de ejecución de O(n_2), ya que estábamos mirando aproximadamente todos los elementos _n para encontrar el más pequeño y realizando n pasadas para ordenar todos los elementos.
-
Más formalmente, podemos utilizar algunas fórmulas para demostrar que el factor más grande es de hecho _n_2:
n + (n – 1) + (n – 2) + ... + 1 n(n + 1)/2 (n^2 + n)/2 n^2/2 + n/2 O(n^2) -
Entonces, resulta que la selección de tipo es básicamente igual que la ordenación de burbuja en tiempo de ejecución:
- O(_n_2)
- Ordenación de burbuja, selección de tipo
- O(n log n)
- O(n)
- Búsqueda lineal
- O(log n)
- Búsqueda binaria
- O(1)
- O(_n_2)
- El mejor caso, Ω, también es _n_2.
-
Podemos volver a la ordenación de burbuja y cambiar su algoritmo a que sea algo como esto, lo que nos permitirá detenernos antes de tiempo si se ordenan todos los elementos:
Repetir hasta que no haya canjes Para i de 0 a n–2 Si los elementos i e i+1 están fuera de orden Canjearlos- Ahora, solo necesitamos mirar cada elemento una vez, por lo que el mejor caso es ahora Ω(n):
- Ω(_n_2)
- Selección de tipo
- Ω(n log n)
- Ω(n)
- Ordenación de burbuja
- Ω(log n)
- Ω(1)
- Búsqueda lineal, búsqueda binaria
- Ω(_n_2)
- Ahora, solo necesitamos mirar cada elemento una vez, por lo que el mejor caso es ahora Ω(n):
-
Consideramos una visualización en línea comparando algoritmos de ordenación con animaciones para ver cómo se mueven los elementos dentro de las matrices para la ordenación de burbuja y la selección de tipo.
Recursión
-
Recuerde que en la semana 0, teníamos pseudocódigo para encontrar un nombre en una guía telefónica. Este pseudocódigo contenía líneas que nos decían "volver" y repetir algunos pasos:
1 Tomar la guía telefónica 2 Abrirla por la mitad 3 Mirar la página 4 Si Smith está en la página 5 Llamar a Mike 6 Sino, si Smith está antes en la guía 7 Abrir por la mitad la mitad izquierda del libro 8 **Volver a la línea 3** 9 Sino si Smith está después en la guía 10 Abrir por la mitad la mitad derecha del libro 11 **Volver a la línea 3** 12 Sino 13 Salir -
En lugar de eso, podríamos repetir todo nuestro algoritmo en la mitad del libro que nos queda:
1 Tomar la guía telefónica 2 Abrirla por la mitad 3 Mirar la página 4 Si Smith está en la página 5 Llamar a Mike 6 Sino, si Smith está antes en la guía 7 **Buscar en la mitad izquierda del libro** 8 9 Sino si Smith está después en la guía 10 **Buscar en la mitad derecha del libro** 11 12 Sino 13 Salir- Esto parece un proceso cíclico que nunca terminará, pero en realidad estamos dividiendo el problema por la mitad cada vez y deteniéndonos una vez que no quede más libro.
-
Recursión ocurre cuando una función o algoritmo se refiere a sí mismo, como en el nuevo pseudocódigo anterior.
-
También en la semana 1, implementamos una "pirámide" de bloques en la siguiente forma:
# ## ### ####-
Y podríamos haber tenido código iterativo como este:
#include <cs50.h> #include <stdio.h> void draw(int h); int main(void) { // Obtener la altura de la pirámide int height = get_int("Altura: "); // Dibujar la pirámide draw(height); } void draw(int h) { // Dibujar una pirámide de altura h for (int i = 1; i <= h; i++) { for (int j = 1; j <= i; j++) { printf("#"); } printf("\n"); } }- Aquí, usamos ciclos
forpara imprimir cada bloque en cada fila.
- Aquí, usamos ciclos
-
-
Pero observe que una pirámide de altura 4 es en realidad una pirámide de altura 3, con una fila adicional de 4 bloques añadida. Y una pirámide de altura 3 es una pirámide de altura 2, con una fila extra de 3 bloques. Una pirámide de altura 2 es una pirámide de altura 1, con una fila adicional de 2 bloques. Y finalmente, una pirámide de altura 1 es solo una pirámide de altura 0, o nada, con otra fila de un solo bloque añadida.
-
Con esta idea en mente, podemos escribir:
#include <cs50.h> #include <stdio.h> void draw(int h); int main(void) { // Obtener la altura de la pirámide int height = get_int("Altura: "); // Dibujar la pirámide draw(height); } void draw(int h) { // Si no hay nada que dibujar if (h == 0) { return; } // Dibujar una pirámide de altura h - 1 draw(h - 1); // Dibujar una fila más de ancho h for (int i = 0; i < h; i++) { printf("#"); } printf("\n"); }- Ahora, nuestra función
drawprimero se llama a sí misma recursivamente, dibujando una pirámide de alturah - 1. Pero incluso antes de eso, necesitamos detenernos sihes 0, ya que no quedará nada por dibujar. - Después, dibujamos la siguiente fila, o una fila de ancho
h.
- Ahora, nuestra función
Merge sort
-
Podemos tomar la idea de la recursión para ordenar, con otro algoritmo llamado merge sort. El pseudocódigo podría ser algo como:
Si solo hay un elemento Devolver Sino Ordenar la mitad izquierda de los elementos Ordenar la mitad derecha de los elementos Fusionar las mitades ordenadas -
Podemos ver esto mejor en la práctica con una lista desordenada:
7 4 5 2 6 3 8 1 -
Primero, ordenaremos la mitad izquierda (los primeros cuatro elementos):
7 4 5 2 | 6 3 8 1 – – – – -
Bueno, para ordenar eso, primero necesitamos ordenar la mitad izquierda de la mitad izquierda:
7 4 | 5 2 | 6 3 8 1 – – -
Ahora, tenemos solo un elemento,
7, en la mitad izquierda, y un elemento,4, en la mitad derecha. Entonces los fusionaremos, tomando el elemento más pequeño de cada lista primero:– – | 5 2 | 6 3 8 1 4 7 -
Y ahora regresamos a la mitad derecha de la mitad izquierda y la ordenamos:
– – | – – | 6 3 8 1 4 7 | 2 5 -
Ahora, ambas mitades de la mitad izquierda están ordenadas, por lo que podemos fusionarlas. Miramos el inicio de cada lista y tomamos
2ya que es más pequeño que4. Después, tomamos4, ya que ahora es el elemento más pequeño en el frente de ambas listas. Después, tomamos5, y finalmente,7, para obtener:– – – – | 6 3 8 1 – – – – 2 4 5 7 -
Ahora ordenamos la mitad derecha de la misma manera. Primero, la mitad izquierda de la mitad derecha:
– – – – | – – | 8 1 – – – – | 3 6 | 2 4 5 7 -
Después, la mitad derecha de la mitad derecha:
– – – – | – – | – – – – – – | 3 6 | 1 8 2 4 5 7 -
Ahora podemos fusionar la mitad derecha:
– – – – | – – – – – – – – | – – – – 2 4 5 7 | 1 3 6 8 -
Y finalmente, podemos fusionar ambas mitades de la lista completa, siguiendo los mismos pasos que antes. Observa que no necesitamos verificar todos los elementos de cada mitad para encontrar el más pequeño, ya que sabemos que cada mitad ya está ordenada. En cambio, solo tomamos el elemento más pequeño de los dos al inicio de cada mitad:
– – – – | – – – – – – – – | – – – – 2 4 5 7 | – 3 6 8 1 – – – – | – – – – – – – – | – – – – – 4 5 7 | – 3 6 8 1 2 – – – – | – – – – – – – – | – – – – – 4 5 7 | – – 6 8 1 2 3 – – – – | – – – – – – – – | – – – – – – 5 7 | – – 6 8 1 2 3 4 – – – – | – – – – – – – – | – – – – – – – 7 | – – 6 8 1 2 3 4 5 – – – – | – – – – – – – – | – – – – – – – 7 | – – – 8 1 2 3 4 5 6 – – – – | – – – – – – – – | – – – – – – – – | – – – 8 1 2 3 4 5 6 7 – – – – | – – – – – – – – | – – – – – – – – | – – – – 1 2 3 4 5 6 7 8 -
Llevó muchos pasos, pero en realidad llevó menos pasos que los otros algoritmos que hemos visto hasta ahora. Dividimos nuestra lista por la mitad cada vez, hasta que estuvimos "ordenando" ocho listas con un elemento cada una:
7 | 4 | 5 | 2 | 6 | 3 | 8 | 1 4 7 | 2 5 | 3 6 | 1 8 2 4 5 7 | 1 3 6 8 1 2 3 4 5 6 7 8 -
Dado que nuestro algoritmo dividía el problema por la mitad cada vez, su tiempo de ejecución es logarítmico con O(log n). Y después de ordenar cada mitad (o la mitad de una mitad), necesitábamos fusionar todos los elementos, con n pasos ya que teníamos que buscar cada elemento una vez.
- Por lo que nuestro tiempo de ejecución total es O(n log n):
- O(_n_2)
- Ordenamiento de burbuja, ordenamiento por selección
- O(n log n)
- Ordenamiento por combinación
- O(n)
- Búsqueda lineal
- O(log n)
- Búsqueda binaria
- O(1)
- O(_n_2)
- Como log n es mayor que 1 pero menor que n, n log n está entre n (veces 1) y _n_2.
- El mejor caso, Ω, sigue siendo n log n, ya que todavía ordenamos cada mitad primero y luego las fusionamos:
- Ω(_n_2)
- Ordenamiento por selección
- Ω(n log n)
- Ordenamiento por combinación
- Ω(n)
- Ordenamiento de burbuja
- Ω(log n)
- Ω(1)
- Búsqueda lineal, búsqueda binaria
- Ω(_n_2)
- Finalmente, hay otra notación, Θ, Theta, que usamos para describir los tiempos de ejecución de los algoritmos si el límite superior y el límite inferior son los mismos. Por ejemplo, el ordenamiento por combinación tiene Θ(n log n) ya que el mejor y el peor caso requieren el mismo número de pasos. Y el ordenamiento por selección tiene Θ(_n_2).
- Vemos una visualización final de algoritmos de ordenamiento con un mayor número de entradas, ejecutándose al mismo tiempo.