Lección 5

Punteros

  • La última vez, aprendimos sobre punteros, malloc y otras herramientas útiles para trabajar con memoria.

  • Revisemos este fragmento de código:

      int main(void)
  {
      int *x;
      int *y;

      x = malloc(sizeof(int));

      *x = 42;
      *y = 13;
  }
    • Aquí, las dos primeras líneas de código en nuestra función main están declarando dos punteros, x e y. Luego, asignamos suficiente memoria para un int con malloc y almacenamos la dirección devuelta por malloc en x.
    • Con *x = 42;, vamos a la dirección apuntada por x y almacenamos el valor 42 en esa ubicación.

    • Sin embargo, la última línea está defectuosa ya que no sabemos cuál es el valor de y, ya que nunca le hemos asignado un valor. En su lugar, podemos escribir:

        y = x;
  *y = 13;
      • Y esto hará que y apunte a la misma ubicación que x y luego establecerá ese valor en 13.

  • Echamos un vistazo a un clip corto, Diversión con punteros con Binky, que también explica este fragmento de una manera animada.

Redimensionando matrices

  • En la semana 2, aprendimos acerca de las matrices, donde pudimos almacenar el mismo tipo de valor en una lista, una al lado de la otra. Pero necesitamos declarar el tamaño de las matrices cuando las creamos, y cuando deseamos aumentar el tamaño de la matriz, la memoria circundante podría estar ocupada por algún otro dato.
  • Una solución podría ser asignar más memoria en un área más grande que esté libre, y mover nuestra matriz allí, donde tiene más espacio. Pero necesitaremos copiar nuestra matriz, lo que se convierte en una operación con tiempo de ejecución de O(n), ya que necesitamos copiar cada uno de los n elementos en una matriz.

  • Podríamos escribir un programa como el siguiente para hacer esto en código:

      #include <stdio.h>
  #include <stdlib.h>

  int main(void)
  {
      // Aquí, asignamos suficiente memoria para que quepan tres enteros, y nuestra variable
      // list apuntará al primer entero.
      int *list = malloc(3 * sizeof(int));
      // Debemos verificar que asignamos la memoria correctamente, ya que malloc podría
      // fallar en obtener suficiente memoria libre.
      if (list == NULL)
      {
          return 1;
      }

      // Con esta sintaxis, el compilador realizará aritmética de punteros por nosotros, y
      // calculará el byte en memoria al que se asigna list[0], list[1] y list[2],
      // ya que los enteros tienen 4 bytes de tamaño.
      list[0] = 1;
      list[1] = 2;
      list[2] = 3;

      // Ahora, si queremos redimensionar nuestra matriz para que quepa 4 enteros, intentaremos asignar
      // suficiente memoria para ellos y temporalmente usaremos tmp para señalar al primero:
      int *tmp = malloc(4 * sizeof(int));
      if (tmp == NULL)
      {
          return 1;
      }

      // Ahora, copiamos enteros de la matriz antigua a la nueva matriz ...
      for (int i = 0; i < 3; i++)
      {
          tmp[i] = list[i];
      }

      // ... y agregamos el cuarto entero:
      tmp[3] = 4;

      // Debemos liberar la memoria original para list, por eso necesitamos un
      // variable temporal para señalar a la nueva matriz ...
      free(list);

      // ... y ahora podemos establecer nuestra variable list para que apunte a la nueva matriz que
      // tmp apunta a:
      list = tmp;

      // Ahora, podemos imprimir la nueva matriz:
      for (int i = 0; i < 4; i++)
      {
          printf("%i\n", list[i]);
      }

      // Y finalmente, libera la memoria para la nueva matriz.
      free(list);
  }

  • Resulta que en realidad hay una función útil, realloc, que reasignará algo de memoria:

      #include <stdio.h>
  #include <stdlib.h>

  int main(void)
  {
      int *list = malloc(3 * sizeof(int));
      if (list == NULL)
      {
          return 1;
      }

      list[0] = 1;
      list[1] = 2;
      list[2] = 3;

      // Aquí, le damos a realloc nuestra matriz original a la que apunta list y
      // devolverá una nueva dirección para una nueva matriz, con los datos antiguos copiados:
      int *tmp = realloc(list, 4 * sizeof(int));
      if (tmp == NULL)
      {
          return 1;
      }
      // Ahora, todo lo que necesitamos hacer es recordar la ubicación de la nueva matriz:
      list = tmp;

      list[3] = 4;

      for (int i = 0; i < 4; i++)
      {
          printf("%i\n", list[i]);
      }

      free(list);
  }

Estructuras de datos

  • Las estructuras de datos son estructuras de programación que nos permiten almacenar información en diferentes diseños en la memoria de nuestro ordenador.
  • Para construir una estructura de datos, necesitaremos algunas herramientas que hemos visto:
    • struct para crear tipos de datos personalizados
    • . para acceder a las propiedades de una estructura
    • * para ir a una dirección de memoria a la que apunta un puntero

Listas Enlazadas

  • Con una lista enlazada, podemos almacenar una lista de valores que pueden crecer fácilmente almacenando valores en diferentes partes de la memoria: cuadrícula que representa la memoria, con tres de las casillas etiquetadas con casillas vacías entre ellas, cada una etiquetada como 1 0x123, 2 0x456 y 3 0x789
    • Esto es diferente a una matriz, ya que nuestros valores ya no están uno al lado del otro en la memoria.
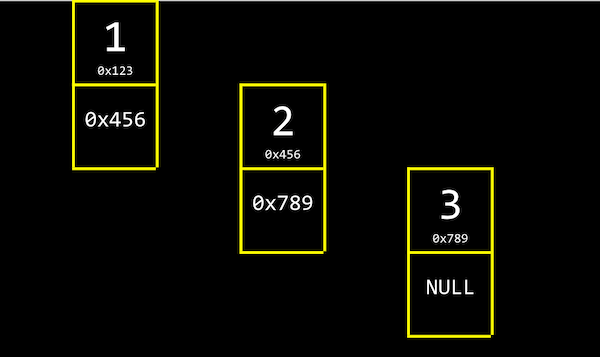
  • Podemos vincular nuestra lista entre sí asignando, para cada elemento, suficiente memoria tanto para el valor que queremos almacenar como para la dirección del siguiente elemento: tres cuadros, cada uno dividido en dos y etiquetado como (1 0x123 y 0x456), (2 0x456 y 0x789) y (3 0x789 y NULL)
    • Por cierto, NUL se refiere a \0, un carácter que termina una cadena, y NULL se refiere a una dirección de todos los ceros, o un puntero nulo que podemos pensar como que no apunta a ninguna parte.
  • A diferencia de los arreglos, ya no podemos acceder aleatoriamente a los elementos de una lista enlazada. Por ejemplo, ya no podemos acceder al quinto elemento de la lista calculando dónde está, en tiempo constante. (Como sabemos que los arreglos almacenan elementos uno al lado del otro, podemos agregar 1, 4 o el tamaño de nuestro elemento para calcular direcciones). En cambio, debemos seguir el puntero de cada elemento, uno a la vez. Y necesitamos asignar el doble de memoria de la que necesitábamos antes para cada elemento.

  • En código, podríamos crear nuestra propia estructura llamada nodo (como un nodo de un gráfico en matemáticas), y necesitamos almacenar un int y un puntero al siguiente nodo llamado siguiente:

      typedef struct node
  {
      int number;
      struct node *next;
  }
  node;
    • Iniciamos esta estructura con typedef struct node para poder referirnos a un nodo dentro de nuestra estructura.

  • Podemos construir una lista enlazada en código comenzando con nuestra estructura. Primero, querremos recordar una lista vacía, por lo que podemos usar el puntero nulo: node *list = NULL;.

  • Para agregar un elemento, primero necesitaremos asignar algo de memoria para un nodo y establecer sus valores:

      node *n = malloc(sizeof(node));
  // Queremos asegurarnos de que malloc haya logrado obtener memoria para nosotros:
  if (n != NULL)
  {
      // Esto es equivalente a (*n).number, donde primero vamos al nodo apuntado
      // por n, y luego establecemos la propiedad numérica. En C, también podemos usar esta
      // notación de flecha:
      n->number = 2;
      // Entonces necesitamos almacenar un puntero al siguiente nodo en nuestra lista, pero el
      // nuevo nodo no apuntará a nada (por ahora):
      n->next = NULL;
  }

  • Ahora nuestra lista puede apuntar a este nodo: list = n;: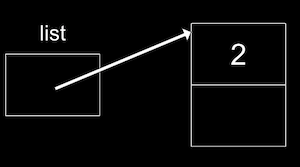 una casilla etiquetada como lista con una flecha hacia afuera que apunta a dos casillas conectadas, una con 2 y otra vacía)

  • Para agregar a la lista, crearemos un nuevo nodo de la misma manera, quizás con el valor 4. Pero ahora necesitamos actualizar el puntero en nuestro primer nodo para que apunte a él.

  • Como nuestro puntero lista solo apunta al primer nodo (y no podemos estar seguros de que la lista solo tenga un nodo), necesitamos "seguir las migas de pan" y seguir el puntero siguiente de cada nodo:

      // Crear un puntero temporal a lo que lista está apuntando
  node *tmp = list;
  // Mientras el nodo tenga un puntero siguiente ...
  while (tmp->next != NULL)
  {
      // ... establecer el temporal al siguiente nodo
      tmp = tmp->next;
  }
  // Ahora, tmp apunta al último nodo de nuestra lista y podemos actualizar su siguiente
  // puntero para que apunte a nuestro nuevo nodo.

  • Si queremos insertar un nodo al principio de nuestra lista enlazada, debemos actualizar cuidadosamente nuestro nodo para que apunte al que lo sigue, antes de actualizar la lista. De lo contrario, perderemos el resto de nuestra lista:

      // Aquí, estamos insertando un nodo en el frente de la lista, por lo que queremos su
  // siguiente puntero para apuntar a la lista original, antes de apuntar la lista a
  // n:
  n->next = list;
  list = n;

  • Y para insertar un nodo en el medio de nuestra lista, podemos recorrer la lista, siguiendo cada elemento uno a la vez, comparando sus valores y cambiando los punteros siguientes con cuidado también.

  • Con algunos voluntarios en el escenario, simulamos una lista, con cada voluntario actuando como la variable lista o un nodo. A medida que insertamos nodos en la lista, necesitamos un puntero temporal para seguir la lista y asegurarnos de no perder ninguna parte de nuestra lista. Nuestra lista enlazada solo apunta al primer nodo de nuestra lista, por lo que solo podemos mirar un nodo a la vez, pero podemos asignar dinámicamente más memoria a medida que necesitemos hacer crecer nuestra lista.

  • Ahora, incluso si nuestra lista enlazada está ordenada, el tiempo de ejecución de su búsqueda será O(n), ya que debemos seguir cada nodo para verificar sus valores y no sabemos dónde estará el medio de nuestra lista.

  • Podemos combinar todos nuestros fragmentos de código en un programa completo:
      #include <stdio.h>
  #include <stdlib.h>

  // Representa un nodo
  typedef struct node
  {
      int number;
      struct node *next;
  }
  node;

  int main(void)
  {
      // Lista de tamaño 0, inicialmente no apunta a nada
      node *list = NULL;

      // Agregar número a la lista
      node *n = malloc(sizeof(node));
      if (n == NULL)
      {
          return 1;
      }
      n->number = 1;
      n->next = NULL;
      // Creamos nuestro primer nodo, almacenamos en él el valor 1 y dejamos que el siguiente
      // puntero no apunte a nada. Entonces, nuestra variable de lista puede apuntar a él.
      list = n;

      // Agregar número a la lista
      n = malloc(sizeof(node));
      if (n == NULL)
      {
          return 1;
      }
      n->number = 2;
      n->next = NULL;
      // Ahora, vamos a nuestro primer nodo al que apunta list y configuramos el siguiente puntero
      // en él para que apunte a nuestro nuevo nodo, agregándolo al final de la lista:
      list->next = n;

      // Agregar número a la lista
      n = malloc(sizeof(node));
      if (n == NULL)
      {
          return 1;
      }
      n->number = 3;
      n->next = NULL;
      // Podemos seguir múltiples nodos con esta sintaxis, usando el siguiente puntero
      // una y otra vez, para agregar nuestro tercer nuevo nodo al final de la lista:
      list->next->next = n;
      // Normalmente, sin embargo, querríamos un bucle y una variable temporal para agregar
      // un nuevo nodo a nuestra lista.

      // Imprimir lista
      // Aquí podemos iterar sobre todos los nodos de nuestra lista con una variable temporal.
      // Primero, tenemos un puntero temporal, tmp, que apunta a la
      // lista. Luego, nuestra condición para continuar es que tmp no es NULL, y
      // finalmente, actualizamos tmp al siguiente puntero de sí mismo.
      for (node *tmp = list; tmp != NULL; tmp = tmp->next)
      {
          // Dentro del nodo, simplemente imprimiremos el número almacenado:
          printf("%i\n", tmp->number);
      }

      // Liberar lista
      // Como vamos liberando cada nodo a medida que avanzamos, usaremos un bucle while
      // y seguiremos el siguiente puntero de cada nodo antes de liberarlo, pero veremos
      // esto con más detalle en el Problema Establecido 5.
      while (list != NULL)
      {
          node *tmp = list->next;
          free(list);
          list = tmp;
      }
  }

Más estructuras de datos

  • Un árbol es otra estructura en la que cada nodo apunta a otro nodo, uno a la izquierda (con valor más pequeño) y otro a la derecha (con valor más grande):
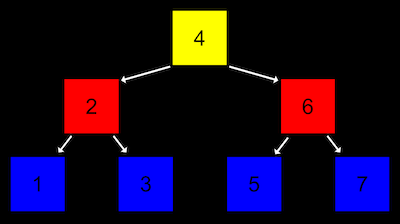
    árbol con nodo 4 en centro superior, flecha izquierda a 3 debajo, flecha derecha a 6 debajo; 2 tiene flecha izquierda a 1 debajo, flecha derecha a 3 debajo; 6 tiene flecha izquierda a 5 debajo, flecha derecha a 7 debajo
    • Observa que ahora hay dos dimensiones en esta estructura, donde algunos nodos están en distintos «niveles» que otros. Podemos implementar esto con una versión más compleja de un nodo en una lista enlazada, donde cada nodo tiene no uno, sino dos punteros, uno para el valor en «la mitad de la mitad izquierda» y otro para el valor en «la mitad de la mitad derecha». Todos los elementos a la izquierda de un nodo son menores, y todos los elementos a la derecha son mayores.
    • Esto se llama un árbol binario de búsqueda porque cada nodo tiene como máximo dos descendientes (nodos a los que apunta) y un árbol de búsqueda porque está ordenado de un modo que nos permite buscar correctamente.
    • Al igual que una lista enlazada, querremos mantener un puntero solo al inicio de la lista, pero en este caso queremos apuntar a la raíz, o nodo superior central del árbol (el 4).

  • Ahora, podemos hacer fácilmente una búsqueda binaria, y puesto que cada nodo apunta a otro, también podemos insertar nodos en el árbol sin tener que moverlos todos, como tendríamos que hacer en un array. Una búsqueda recursiva de este árbol podría parecerse a lo siguiente:

      typedef struct node
  {
      int number;
      struct node *left;
      struct node *right;
  } node;

  // Aquí, *tree es un puntero a la raíz de nuestro árbol.
  bool search(node *tree)
  {
      // Necesitamos un caso base: si el árbol actual (o parte del árbol) es NULL,
      // devolverá false:
      if (tree == NULL)
      {
          return false;
      }
      // Ahora, en función de si el número del nodo actual es mayor o menor,
      // podemos mirar el lado izquierdo o derecho del árbol:
      else if (50 < tree->number)
      {
          return search(tree->left);
      }
      else if (50 > tree->number)
      {
          return search(tree->right);
      }
      // De lo contrario, el número debe ser igual al que buscamos:
      else {
          return true;
      }
  }

  • El tiempo de ejecución de la búsqueda de un árbol es O(log n), e insertar nodos mientras se mantiene el árbol equilibrado también es O(log n). Al dedicar un poco más de memoria y tiempo al mantenimiento del árbol, ahora tenemos una búsqueda más rápida en comparación con una lista vinculada simple.

  • Una estructura de datos con un tiempo de búsqueda casi constante es una tabla hash, que es una combinación de una matriz y una lista vinculada. Tenemos una matriz de listas vinculadas, y cada lista vinculada en la matriz tiene elementos de una categoría determinada. Por ejemplo, en el mundo real podríamos tener muchas etiquetas de nombre y podríamos ordenarlas en 26 cubos, uno etiquetado con cada letra del alfabeto, para poder encontrar etiquetas de nombre mirando solo en un cubo.
  • Podemos implementar esto en una tabla hash con una matriz de 26 punteros, cada uno de los cuales apunta a una lista vinculada para una letra del alfabeto: [matriz vertical con 26 cajas, la primera con una flecha que apunta a una caja etiquetada como Albus, la segunda vacía, la tercera con una flecha que apunta a una caja etiquetada como Cedric ... la séptima con una flecha que apunta a una caja etiquetada como Ginny con una flecha desde esa caja apuntando a una caja etiquetada como George ...] (https://cs50.harvard.edu/x/2020/notes/5/hash_table.png)
  • Como tenemos acceso aleatorio con matrices, podemos agregar elementos rápidamente y también indexar rápidamente en un cubo.
  • Un cubo puede tener varios valores coincidentes, por lo que usaremos una lista vinculada para almacenarlos todos horizontalmente. (A esto lo llamamos una colisión, cuando dos valores coinciden de alguna manera).
  • A esto se le llama tabla hash porque usamos una función hash, que toma alguna entrada y la mapea a un cubo en el que debería ir. En nuestro ejemplo, la función hash solo mira la primera letra del nombre, por lo que podría devolver '0' para "Albus" y '25' para "Zacharias".
  • Pero en el peor de los casos, todos los nombres pueden comenzar con la misma letra, por lo que podríamos terminar con el equivalente a una sola lista vinculada nuevamente. Podríamos mirar las dos primeras letras y asignar suficientes cubos para 26 * 26 posibles valores hash, o incluso las primeras tres letras, y ahora necesitaremos 26 * 26 * 26 cubos. Pero aún podríamos tener un peor caso en el que todos nuestros valores comiencen con los mismos tres caracteres, por lo que el tiempo de ejecución para la búsqueda es O(n). Sin embargo, en la práctica, podemos acercarnos a O(1) si tenemos aproximadamente tantos cubos como valores posibles, especialmente si tenemos una función hash ideal, donde podemos ordenar nuestras entradas en cubos únicos.
  • Podemos usar otra estructura de datos llamada trie (que se pronuncia como "intentar", y es la abreviatura de "recuperación"): [matriz con letras de la A a la Z en 26 elementos, con H apuntando a otra matriz con las 26 letras. La A y la E de esta matriz apuntan cada una a dos matrices más de las 26 letras, y esto continúa en un árbol hasta que las matrices más bajas sólo tienen una letra marcada como válida] (https://cs50.harvard.edu/x/2020/notes /5/trie.png)
  • Imagina que queremos almacenar un diccionario de palabras de manera eficiente y poder acceder a cada una de ellas en tiempo constante. Un trie es como un árbol, pero cada nodo es una matriz. Cada matriz tendrá cada letra, de la A a la Z, almacenada. Para cada palabra, la primera letra apuntará a una matriz, donde la siguiente letra válida apuntará a otra matriz, y así sucesivamente, hasta que lleguemos a algo que indique el final de una palabra válida. Si nuestra palabra no está en el trie, entonces una de las matrices no tendrá un puntero o carácter de terminación para nuestra palabra. Ahora, incluso si nuestra estructura de datos tiene muchas palabras, el tiempo de búsqueda será solo la longitud de la palabra que estamos buscando, y este podría ser un máximo fijo, por lo que tenemos O(1) para búsqueda e inserción. Sin embargo, el costo de esto es 26 veces más memoria de la que necesitamos para cada carácter.
  • Hay construcciones de nivel aún más alto, estructuras de datos abstractas, donde usamos nuestros bloques de construcción de matrices, listas vinculadas, tablas hash e intentamos implementar una solución a algún problema.
  • Por ejemplo, una estructura de datos abstracta es una cola, donde queremos poder agregar valores y eliminar valores en una forma de primero en entrar, primero en salir (FIFO). Para agregar un valor, podemos ponerlo en cola, y para eliminar un valor, lo sacaríamos de la cola. Y podemos implementar esto con una matriz que redimensionamos a medida que agregamos elementos, o una lista vinculada donde agregamos valores al final.
  • Una estructura de datos "opuesta" sería una pila, donde los elementos añadidos más recientemente (empujados) se eliminan (extraídos) primero, en una forma de último en entrar, primero en salir (LIFO). Nuestra bandeja de entrada de correo electrónico es una pila, donde nuestros correos electrónicos más recientes están en la parte superior.
  • Otro ejemplo es un diccionario, donde podemos mapear claves a valores o cadenas a valores, y podemos implementar uno con una tabla hash donde una palabra viene con alguna otra información (como su definición o significado).
  • Echamos un vistazo a ["Jack Learns the Facts About Queues and Stacks"] (https://www.youtube.com/watch?v=2wM6_PuBIxY), una animación sobre estas estructuras de datos.