Tideman

Problema a resolver

Ya conoces las elecciones de pluralidad, que siguen un algoritmo muy simple para determinar el ganador de una elección: cada votante obtiene un voto y el candidato con la mayor cantidad de votos gana.

Pero el voto de pluralidad tiene algunas desventajas. ¿Qué pasa, por ejemplo, en una elección con tres candidatos y se emiten las siguientes papeletas?

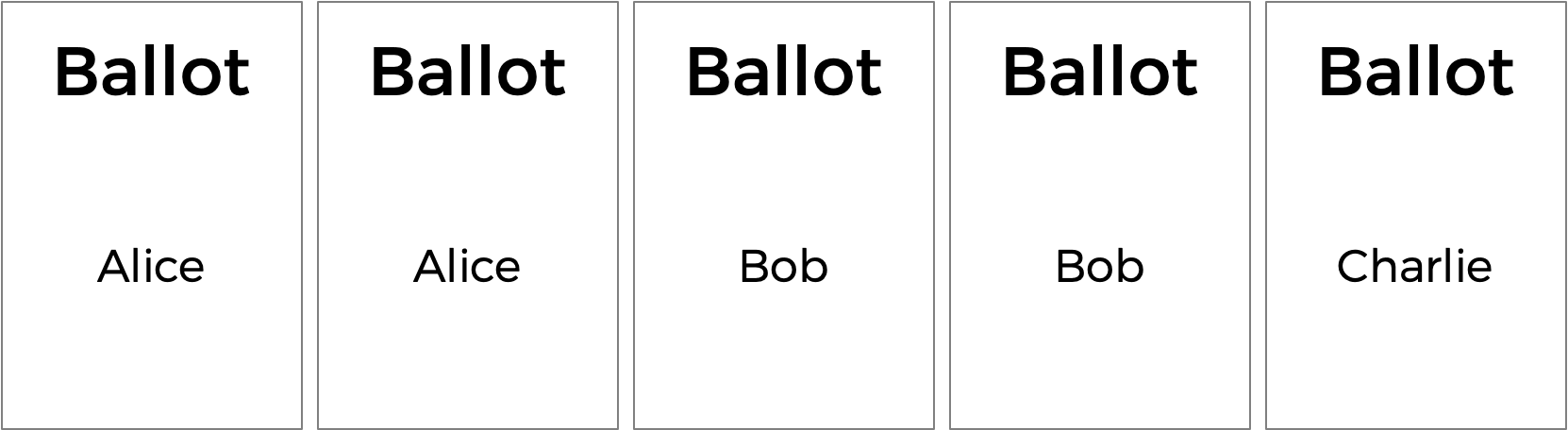
Un voto de pluralidad declararía aquí un empate entre Alice y Bob, ya que cada uno tiene dos votos. Pero, ¿es ese el resultado correcto?

Existe otro tipo de sistema de votación conocido como sistema de votación por orden de preferencia. En un sistema de votación por orden de preferencia, los votantes pueden votar por más de un candidato. En lugar de simplemente votar por su primera opción, pueden clasificar a los candidatos en orden de preferencia. Por lo tanto, las papeletas resultantes podrían verse como las siguientes.

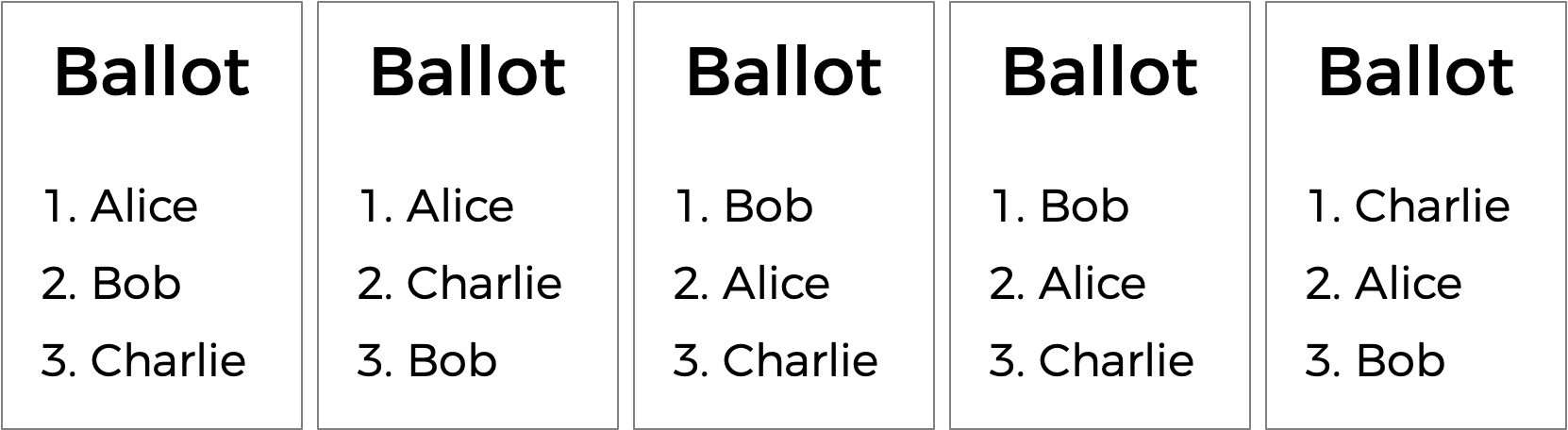
Aquí, cada votante, además de especificar su candidato de primera preferencia, también ha indicado sus segunda y tercera opciones. Y ahora, lo que antes era una elección empatada podría tener un ganador. La carrera inicialmente estaba empatada entre Alice y Bob. Pero el votante que eligió a Charlie prefirió a Alice en lugar de Bob, por lo que Alice podría ser declarada ganadora aquí.

La votación preferencial también puede resolver otro posible inconveniente de la votación por pluralidad. Echa un vistazo a las siguientes papeletas.

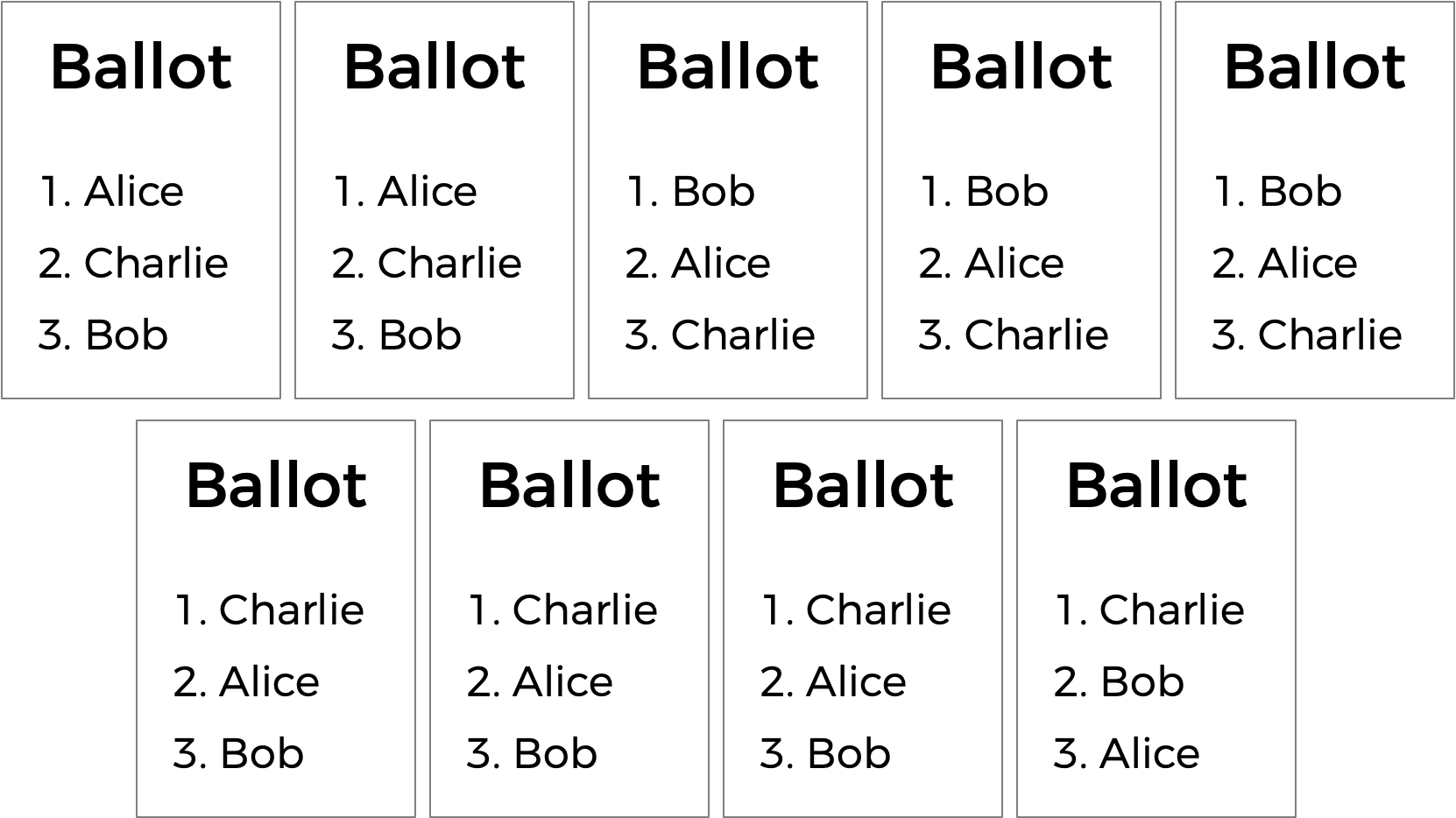
¿Quién debería ganar esta elección? En una votación de pluralidad donde cada votante elige solo su primera preferencia, Charlie gana esta elección con cuatro votos en comparación con solo tres para Bob y dos para Alice. (Ten en cuenta que, si estás familiarizado con el sistema de votación por eliminación instantánea, Charlie también gana aquí bajo ese sistema). Sin embargo, Alice podría argumentar razonablemente que ella debería ser la ganadora de la elección en lugar de Charlie: después de todo, de los nueve votantes, una mayoría (cinco de ellos) prefirió a Alice sobre Charlie, por lo que la mayoría de las personas estaría más feliz con Alice como ganadora en lugar de Charlie.

Alice es, en esta elección, la llamada "ganadora de Condorcet" de la elección: la persona que habría ganado cualquier enfrentamiento directo contra otro candidato. Si la elección hubiera sido solo entre Alice y Bob, o solo entre Alice y Charlie, Alice habría ganado.

El método de votación de Tideman (también conocido como "pares clasificados") es un método de votación preferencial que garantiza que se produzca el ganador de Condorcet de la elección si existe. En un archivo llamado tideman.c en una carpeta llamada tideman, crea un programa para simular una elección mediante el método de votación de Tideman.

Demostración

Código de distribución

Inicia sesión en cs50.dev, haz clic en la ventana del terminal y ejecuta cd por sí solo. Verás que el indicador de la ventana de terminal se asemeja al siguiente:

  $

Luego, ejecuta

  wget https://cdn.cs50.net/2023/fall/psets/3/tideman.zip

para descargar un archivo ZIP llamado tideman.zip en tu espacio de códigos.

Luego, ejecuta

  unzip tideman.zip

para crear una carpeta llamada tideman. Ya no necesitas el archivo ZIP, por lo que puedes ejecutar

  rm tideman.zip

y responder con "y" seguido de Enter en el indicador para eliminar el archivo ZIP que descargaste.

Ahora, escribe

  cd tideman

seguido de Enter para moverte al directorio (es decir, abrirlo). Tu indicador ahora debería verse como el siguiente.

  tideman/ $

Si todo fue exitoso, deberías ejecutar

  ls

y ver un archivo llamado tideman.c. Al ejecutar code tideman.c deberías abrir el archivo donde escribirás tu código para este conjunto de problemas. Si no es así, ¡vuelve sobre tus pasos y trata de determinar dónde te equivocaste!

Antecedentes

En términos generales, el método de Tideman funciona mediante la construcción de un "gráfico" de candidatos, donde una flecha (es decir, un borde) del candidato A al candidato B indica que el candidato A gana contra el candidato B en una confrontación directa. Entonces, el gráfico para la elección anterior se vería como el que sigue.

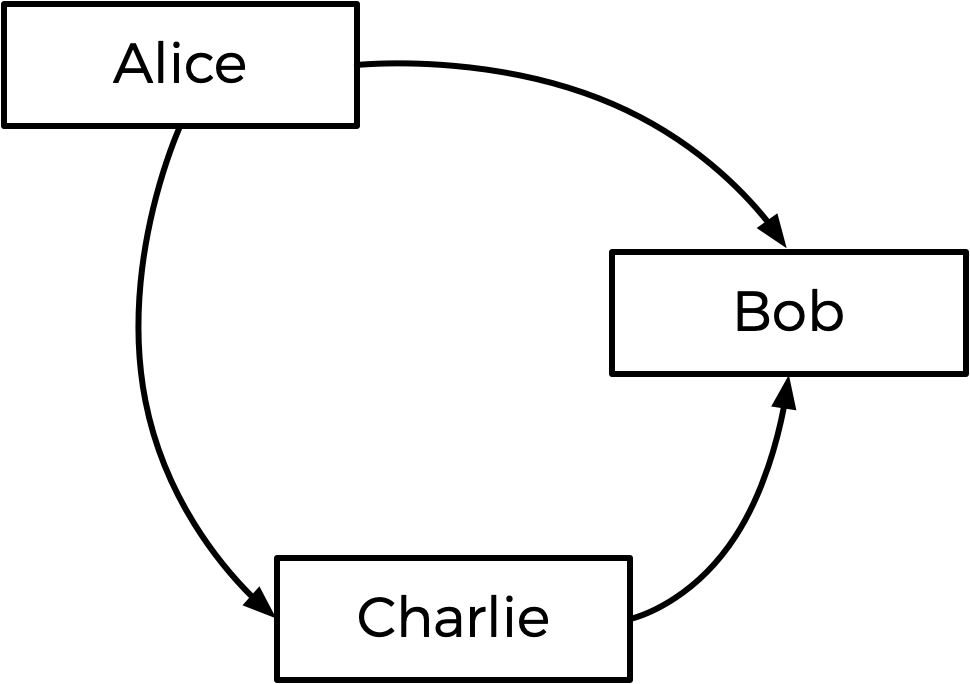
La flecha de Alice a Bob significa que más votantes prefieren a Alice que a Bob (5 prefieren a Alice, 4 prefieren a Bob). Del mismo modo, las otras flechas significan que más votantes prefieren a Alice que a Charlie, y más votantes prefieren a Charlie que a Bob.

Al observar este gráfico, el método de Tideman establece que el ganador de la elección debería ser la "fuente" del gráfico (es decir, el candidato que no tiene ninguna flecha apuntándole). En este caso, la fuente es Alice: Alice es la única que no tiene flechas apuntándola, lo que significa que nadie es preferido en una confrontación directa sobre Alice. Por lo tanto, Alice es declarada ganadora de la elección.

Sin embargo, es posible que cuando se dibujen las flechas, no haya un ganador de Condorcet. Considera las siguientes papeletas.

Entre Alice y Bob, Alice es preferida a Bob por un margen de 7 a 2. Entre Bob y Charlie, Bob es preferido sobre Charlie por un margen de 5 a 4. Pero entre Charlie y Alice, Charlie es preferido sobre Alice por un margen de 6 a 3. Si dibujamos el gráfico, ¡no hay fuente! Tenemos un ciclo de candidatos, donde Alice vence a Bob, quien vence a Charlie, quien vence a Alice (muy parecido a un juego de piedra-papel-tijera). En este caso, parece que no hay forma de elegir un ganador.

Para manejar esto, el algoritmo de Tideman debe tener cuidado de evitar crear ciclos en el gráfico candidato. ¿Cómo lo hace? El algoritmo bloquea primero los bordes más fuertes, ya que posiblemente esos sean los más significativos. En particular, el algoritmo de Tideman especifica que los bordes de emparejamiento deben "bloquearse" en el gráfico uno a la vez, según la "fuerza" de la victoria (cuantas más personas prefieran a un candidato sobre su oponente, más fuerte será la victoria). Siempre que el borde se pueda bloquear en el gráfico sin crear un ciclo, se agrega el borde; de lo contrario, el borde se ignora.

¿Cómo funcionaría esto en el caso de los votos anteriores? Bueno, el mayor margen de victoria para un par es Alice venciendo a Bob, ya que 7 votantes prefieren a Alice sobre Bob (ningún otro enfrentamiento tiene un ganador preferido por más de 7 votantes). Entonces, la flecha de Alice-Bob se bloquea primero en el gráfico. El siguiente mayor margen de victoria es la victoria de Charlie sobre Alice de 6 a 3, por lo que esa flecha se bloquea a continuación.

El siguiente es la victoria de Bob sobre Charlie por 5 a 4. Pero fíjate: ¡si agregáramos una flecha de Bob a Charlie ahora, crearíamos un ciclo! Como el gráfico no permite ciclos, deberíamos omitir este borde y no agregarlo al gráfico en absoluto. Si hubiera más flechas a considerar, miraríamos esas a continuación, pero esa fue la última flecha, por lo que el gráfico está completo.

Este proceso paso a paso se muestra a continuación, con el gráfico final a la derecha.

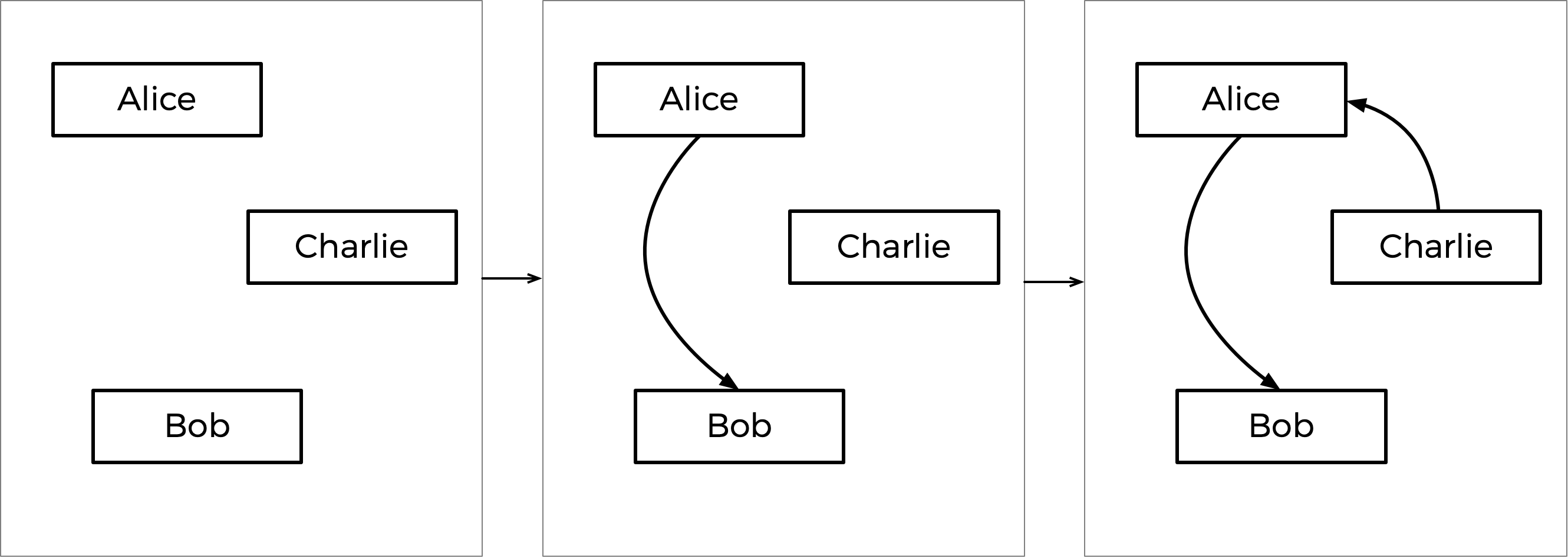
Según el gráfico resultante, Charlie es la fuente (no hay ninguna flecha apuntando hacia Charlie), por lo que Charlie es declarado ganador de esta elección.

Dicho de manera más formal, el método de votación de Tideman consta de tres partes:

• Conteo: una vez que todos los votantes hayan indicado todas sus preferencias, determina, para cada par de candidatos, quién es el candidato preferido y por qué margen es preferido.
• Clasificar: clasifica los pares de candidatos en orden decreciente de fuerza de victoria, donde la fuerza de victoria se define como el número de votantes que prefieren al candidato preferido.
• Bloquear: comenzando con el par más fuerte, recorre los pares de candidatos en orden y "bloquea" cada par en el gráfico de candidatos, siempre que bloquear ese par no cree un ciclo en el gráfico.

Una vez que se completa el gráfico, ¡la fuente del gráfico (la que no tiene bordes apuntando hacia ella) es la ganadora!

Entendiendo

Echemos un vistazo a tideman.c.

Primero, observe la matriz bidimensional preferencias. El entero preferencias[i][j] representará el número de votantes que prefieren al candidato i sobre el candidato j.

El archivo también define otra matriz bidimensional, llamada bloqueada, que representará el gráfico de candidatos. bloqueada es una matriz booleana, por lo que bloqueada[i][j] al ser verdadero representa la existencia de un borde que apunta del candidato i al candidato j; falso significa que no hay un borde. (Si tiene curiosidad, esta representación de un gráfico se conoce como una "matriz de adyacencia").

Lo siguiente es un struct llamado par, usado para representar un par de candidatos: cada par incluye el índice de candidato del ganador y el índice de candidato del perdedor.

Los candidatos mismos se almacenan en la matriz candidatos, la cual es una matriz de cadenas que representan los nombres de cada uno de los candidatos. También hay una matriz de pares, la cual representará todos los pares de candidatos (para los cuales uno es preferido sobre el otro) en la elección.

El programa también tiene dos variables globales: cantidad_pares y cantidad_candidatos, representando la cantidad de pares y la cantidad de candidatos en las matrices pares y candidatos, respectivamente.

Ahora en main. Observe que después de determinar la cantidad de candidatos, el programa recorre el gráfico bloqueado e inicialmente establece todos los valores en falso, lo que significa que nuestro gráfico inicial no tendrá bordes en él.

Después, el programa recorre todos los votantes y recolecta sus preferencias en una matriz llamada rangos (mediante una llamada a voto), donde rangos[i] es el índice del candidato que es la preferencia i para el votante. Estos rangos son pasados a la función registrar_preferencia, cuyo trabajo es tomar esos rangos y actualizar la variable global preferencias.

Una vez que todos los votos están dentro, los pares de candidatos se añaden a la matriz pares mediante una llamada a añadir_pares, clasificada mediante una llamada a ordenar_pares y bloqueada en el gráfico mediante una llamada a bloquear_pares. ¡Finalmente, se llama a mostrar_ganador para imprimir el nombre del ganador de la elección!

Más abajo en el archivo, verá que las funciones voto, registrar_preferencia, añadir_pares, ordenar_pares, bloquear_pares y mostrar_ganador se dejan en blanco. ¡Eso depende de usted!

Especificaciones

Complete la implementación de tideman.c de tal manera que simule una elección de Tideman.

• Complete la función voto.
  • La función toma los argumentos rango, nombre y rangos. Si nombre coincide con el nombre de un candidato válido, entonces debe actualizar la matriz rangos para indicar que el votante tiene al candidato como su preferencia rango (donde 0 es la primera preferencia, 1 es la segunda preferencia, etc.).
  • Recuerde que rangos[i] aquí representa la preferencia i del usuario.
  • La función debe regresar verdadero si el rango se registró exitosamente, y falso de otra manera (si, por ejemplo, nombre no es el nombre de uno de los candidatos).
  • Puede asumir que no hay dos candidatos con el mismo nombre.
• Complete la función registrar_preferencias.
  • La función se llama una vez por cada votante, y toma como argumento la matriz rangos, (recuerde que rangos[i] es la preferencia i del votante, donde rangos[0] es la primera preferencia).
  • La función debe actualizar la matriz global preferencias para añadir las preferencias del votante actual. Recuerde que preferencias[i][j] debe representar el número de votantes que prefieren al candidato i sobre el candidato j.
  • Puede asumir que cada votante clasificará a cada uno de los candidatos.
• Complete la función añadir_pares.
  • La función debe añadir todos los pares de candidatos donde un candidato es preferido a la matriz pares. Un par de candidatos que están empatados (uno no es preferido sobre el otro) no debe ser añadido a la matriz.
  • La función debe actualizar la variable global cantidad_pares para que sea el número de pares de candidatos. (Los pares deben, por lo tanto, almacenarse todos entre pares[0] y pares[cantidad_pares - 1], inclusive).
• Complete la función ordenar_pares.
  • La función debe ordenar la matriz pares en orden decreciente de fuerza de victoria, donde la fuerza de victoria se define como el número de votantes que prefieren al candidato preferido. Si múltiples pares tienen la misma fuerza de victoria, puede asumir que el orden no importa.
• Complete la función bloquear_pares.
  • La función debe crear el gráfico bloqueado, añadiendo todos los bordes en orden decreciente de fuerza de victoria siempre y cuando el borde no cree un ciclo.
• Complete la función mostrar_ganador.
  • La función debe imprimir el nombre del candidato que es la fuente del gráfico. Puede asumir que no habrá más de una fuente.

No debe modificar nada más en tideman.c aparte de las implementaciones de las funciones voto, registrar_preferencias, añadir_pares, ordenar_pares, bloquear_pares y mostrar_ganador (y la inclusión de archivos de cabecera adicionales, si así lo desea). Se le permite añadir funciones adicionales a tideman.c, siempre y cuando no cambie las declaraciones de ninguna de las funciones existentes.

Tutorial

Cómo probar

Asegúrese de probar su código para asegurarse de que maneja...

• Una elección con cualquier número de candidatos (hasta el MAX de 9)
• Votación por un candidato por nombre
• Votos inválidos para candidatos que no están en la boleta
• Impresión del ganador de la elección

Correctitud

  check50 cs50/problems/2024/x/tideman

Estilo

  style50 tideman.c

Cómo enviar

  submit50 cs50/problems/2024/x/tideman